惯导初始对准方法讨论
对目前一些比较典型的SINS初始自对准方法进行了仿真和实际数据处理,将对准结果作在一个图上便于比较。算法主要包括以下6种:
(1)i0 pos: 基于惯性系双重积分(位置)算法,
参见“基于频域分离算子的SINS抗晃动干扰初始对准算法.宇航学报,2011 ”
(2)i0 vel: 基于惯性系一次积分(速度)算法,参见同上
(3)i0 Whaba: 基于惯性系的所谓Whaba最优矩阵求解算法,
参见“纬度未知条件下捷联惯导晃动基座的初始对准.航空学报,2012 ”
(4)Kalman fn: 基于比力量测的Kalman滤波算法,姿态反馈修正,
参见“捷联惯导系统静基座初始对准精度分析及仿真.计算机仿真,2006 ”
(5)Kalman vn: 基于速度量测的Kalman滤波算法,姿态速度反馈修正,比较经典,文献可多了。
(6)gyro compass: 捷联罗经初始对准算法,
参见“逆向导航算法及其在捷联罗经动基座初始对准中的应用.CCC2008 ”
1、仿真
仿真条件:陀螺随机常值漂移0.01arcdeg/h;加速度计偏值50ug,为了彰显确定性对准误差的规律,两者的随机游走噪声都设得比较小些。
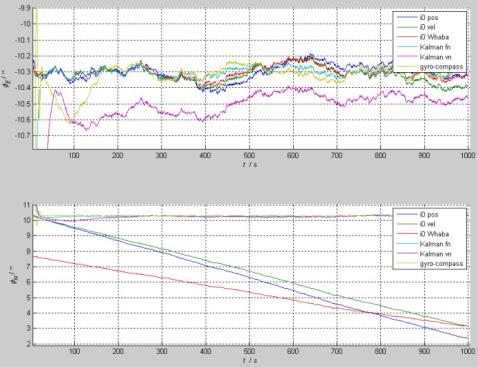
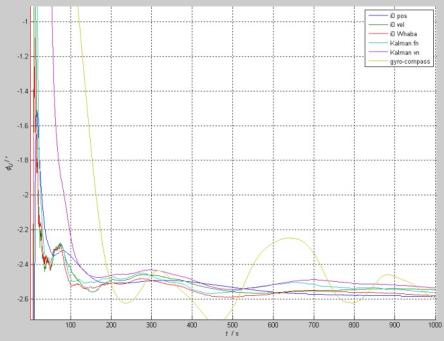
(1)东向和北向平台误差:
分析:东向平台误差在各种方法之间差别都很小,在0.2arcsec之内;但北向平台误差中惯性系对准的三种方法都存在明显的漂移趋势,1000s时漂了多达8arcsec,这主要由陀螺漂移引起的,详见“间接解析自对准算法误差分析,系统工程与电子技术,2013”。
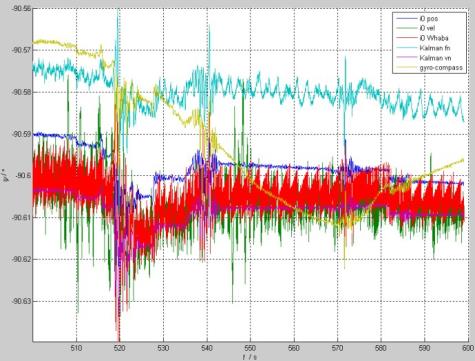
(2)天向平台误差:
分析:罗经对准的方位误差波动比较大,但如果罗经时间参数设置长一些,波动也会相应小些,实际中这是比较难调整的。其他对准方法之间误差差别在0.05arcmin=3arcsec以内,收敛速度也没有明显区别。
2、实际数据处理
条件:惯性级SIMU放置在面包车上,开发动机并实施上下车、开关车门等干扰,从下面的姿态角中可以大致看出晃动干扰的强度。由于没有真实的姿态参考基准,所以不能比较各种对准方法的精度优劣,而只能说明它们的一致性效果。
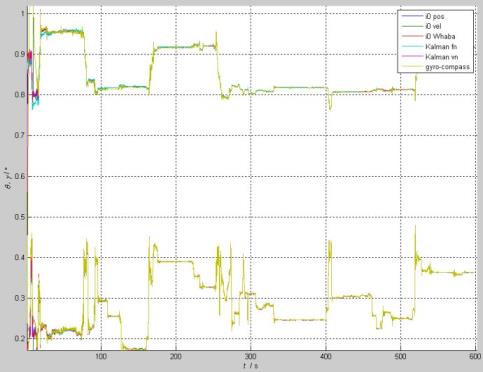
(1)俯仰和横滚姿态角:
(2)东向和北向平台误差:(由于没有真实姿态,这里以Kalman vn对准结果作为参考基准,作图查看其它方法与Kalman vn的差别)
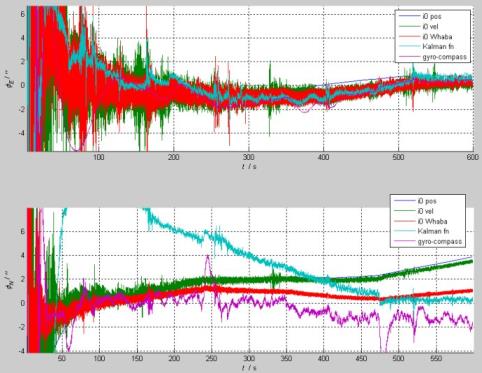
分析:东向失准角差别不大,在1-2arcsec之内;北向失准角中惯性系i0 pos和i0 vel两种方法存在较明显的漂移趋势,600s时多达4arcsec。罗经对准法的时间参数如果再加大(图中对准时取150s),波动会更小些。
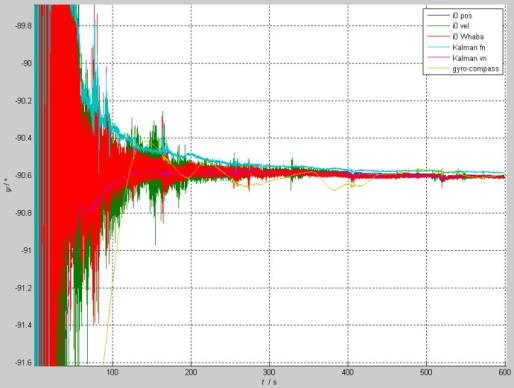
(3a)对准方位角:
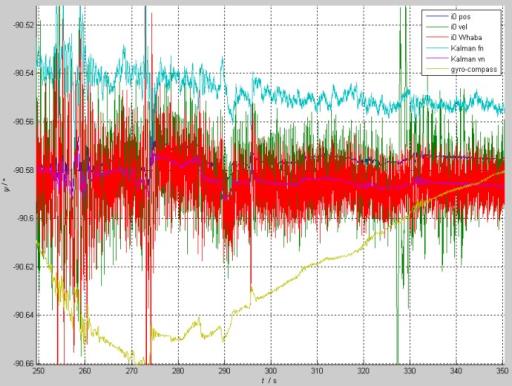
(3b)方位角在300s附近放大图:
(3c)方位角在600s附近放大图:
分析:i0 vel和i0 Wahba方法的方位噪声相对比较大些,而i0 pos、Kalman vn和gyro compass的噪声都比较小。罗经方位波动大也与时间参数设置有关,可通过增大时间参数减小波动;i0 pos和Kalman vn方法在300s后差别约为0.01arcdeg=0.6arcmin,相对陀螺精度而言这一差别基本可以忽略。为何只是Kalman fn方法的方位远离其它方法?
(1)Kalman fn/vn和gyro compass方法都需要先进行粗对准,获得粗略姿态阵,在前面数据处理时我是已知直接给出的,但实际使用时粗略值未知,没法避免这一问题,特别在较强烈 的晃动干扰下,传统解析式对准不可用,一般得先用惯性系方法才能完成粗对准。先粗对准再精对准必然使总的对准时间变长。如果时间十分紧迫的话,可以采用存 储数据和逆向导航的方法,这至少可以节省粗对准的时间。
(2)晃动干扰下,惯性系对准方法不仅可以用于粗对准,还可将其直接用于精对准,时间稍长些的话对准精度通常还算是比较高的,但惯性系方法的一个弱点是:时间越长陀螺漂移会引起北向失准角漂移误差越来越大(几个角秒量级)。
(3)惯性系和gyro compass方法都没有对惯性器件误差建模,在静基座下对准没什么问题,反正器件误差该不可观测的还是不可观,提高不了对准精度;但是如果是基座有比较 大角度的转动,这时有些器件误差变为可观测的了,若采用Kalman滤波的对准方法就更有优势了,对准精度会比没建模的方法更高些。
(4)gyro compass对准方法不好之处是调节时间选取困难,一般必须事先知道对准时间多长,再按其设计相应的调节时间。如果在实际对准过程中延长了时间,而调节 时间很难临时改变,则没法进一步平滑提高对准精度;如果实际对准时间缩短了,则有可能还没来得及完成对准。不象Kalman滤波一样,有多长初始对准时间 它就对准多久,滤波增益自动调节,理论上时间越长收敛精度越高。
(5)前面试验没给出非线性对准方法,可以稍微说明一下。在大失准角误差下,用非线性对准开环不反馈修正的话一般很难达到极限对准精度,因而最好是采用反 馈方式,只要反馈的话水平失准角很快就会收敛变小的。可见,三个失准角均假设为很大的误差模型并不是非常必要,一般只需考虑大方位失准角即可。大方位失准 角非线性对准的前期收敛较慢,信息利用率低有些浪费,所以要快速高精度实现对准的话还是小失准角模型最佳。参见“简化UKF滤波在SINS大失准角初始对准中的应用. 中国惯性技术学报,2008 ”。
(6)初始对准滤波算法比较多,比如经典的KF、EKF以及时髦的UKF、PF、CKF、GHKF等,还可杂交或配上UDU、平方根、SVD分解、遗忘、 自适应、强跟踪、鲁棒、抗差算法等等。在小失准角和模型准确的情况下,KF结果是最优的,言外之意,如果仿真发现有另一种滤波方法比KF还好,那么必然是 在某个环节上出现理论或人为假设错误了。因此,在设计其它算法时,可以先初步在小失准角和模型准确的情况下与KF做个仿真结果对比。
(7)i0 pos和Kalman vn对准方法的精度是比较稳定的、噪声也小,晃动和转动基座下,先用i0 pos粗对准再用Kalman vn精对准是一个非常理想的选择。如果需要快速的话,就加上逆向导航算法可以节省粗对准时间。
(8)基座干扰、对准快速、精度高是相互矛盾的,想要实现快速高精度初始对准,只能要求基座平稳并且传感器噪声水平低才行。贪婪不能是无止境的。目前还没有发现通用公式,给出什么样精度的IMU在多大基座干扰下在多长时间内能够实现多高精度的对准效果。
(9)有些人还研究神经网络、遗传、SVM、退火、蚁群/鱼群等五花八门的方法用于初始对准,我没有仔细研究过,但总感觉不是太靠谱,那些方法适用于不好 用解析表达式表示的非线性问题的寻优,但惯导对准问题模型是很明确的,不需要那些方法,纯粹是把问题复杂化,实际效果并不会更好。
对于几个比较经典的初始对准在“SINS工具箱介绍—各种初始对准方法”中说明讨论过了,这里再给出其它一些算法的看法。
(1)最小二乘参数辨识精对准:当初始失准角稍大时模型存在一定的非线性误差,不能达到对准的极限精度;对准过程中没法采用如Kalman滤波一样的反馈修正的方法降低失准角误差。
(2)根据水平角收敛的斜率提取方位误差的对准方法:理想的仿真效果还可以,但基座扰动或传感器噪声稍大时,还是很难在短时间内实现方位对准,不具实用性。
(3)IMM 交互多模型算法:在大方位失准角下应该还是挺有用的,比如构造36个模型,将不确定性的方位360度均分,则其必有一个模型的方位失准角误差不大于5度, 可视为小失准角误差了,当36个模型同时对准完后(计算量略有点大哦),按一定原则从对准结果中挑出一个正确的就行了。这里每个模型算法都是一样的,只是 方位初始值选取不一样而已。(以上描述好像只有“多模型”没有“交互”的意思,实际上选一个结果也就足够了,别的信息也是多余的)。如果将IMM用于大失准角,那么三个大失准角都划分成小角度再排列组合的话总模型个数就有点太多了,所以不合适。
(4)待续...